Bir Mekanizmada Bulunan Bağımsız Devre Sayısı
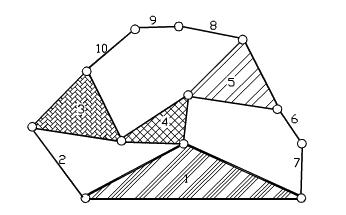
Uzuv sayısı l ve mafsal sayısı j olan bir kinematik zinciri ele alalım. Yukarıda gösterilen örnek 10 uzuvlu (l=10) 12 mafsallı (j=12) bir mekanizma görülmektedir.
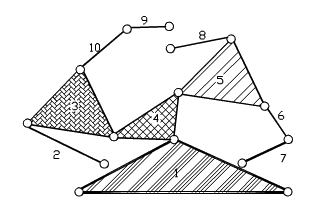
1-2 , 8-9 ve 1-7 numaralı uzuvlar arasında bulunan mafsalları sökelim (isterseniz siz değişik mafsalları sökün). Sökme sırasında kural hiç bir uzuv boşta (zincire bağlanmamış olarak) kalmayacak ve sökme işlemine mekanizmada devre kalmayana kadar (açık kinematik zincir oluşana kadar) edilecektir. Sökülen mafsallar değişik olabilir, ancak kinematik zinciri açık hale getirmek, hiç bir devre bırakmamak için sökülmesi gereken mafsal sayısı daima aynı olacaktır.
Sökülen mafsal sayısı daima kinematik zincirde bulunan devre sayısına eşittir (Devre sayısını L ile gösterelim. Şekilde gösterilen mekanizma için L=3 olur). Elde edilen açık kinematik zincirlerde uzuv sayısı yine başlangıç zincirinde olduğu gibi l dir ancak kalan mafsal sayısı uzuv sayısından bir eksik (l-1) olacaktır (yukarıdaki örneğimizde kalan mafsal sayısı 9 dur)
Mafsal sayısı j olduğuna göre:
j = Açık kinematik zincirde mafsal sayısı + Sökülen mafsal sayısı
j = (l-1) + L
veya
L = j - l + 1
Bu basit fakat çok önemli denklem Euler tarafından bulunmuştur (Euler'in çokgen denklemi) ve bir mekanizmada bağımsız devre kapalılık denklemi sayısını belirlemek için kullanılabilir. Ancak bu, yazacağımız denklemlerin birbirlerinden bağımlı veya bağımsız olup olmadığını gösteremez. Bunu bizim kontrol etmemiz gereklidir (bir devre diğer devrelerin toplamı veya farkı ile elde edilebiliyor ise, bağımlı devredir). Her devre için yazılan vektör devre denkemi iki skaler denklemi oluşturduğundan toplam 2L denklem elde edilir. Bu denklemlerde hareketin kinematik olarak belirli olması için 2L+F kadar konum parametresi bulunmalıdır (F=mekanizma serbestlik derecesi).
|
Not: 1. Devre sayısı mafsal tipine bağlı değildir 2. Devre sayısı uzay serbestlik derecesine bağlı değildir 3. Devre sayısı mekanizma serbestlik derecesine bağlı değildir |
Örnek:
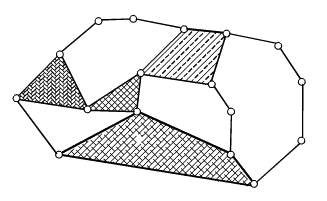
Yukarıda gösterilmiş olan kinematik zincirde kaç bağımsız devre vardır?
Cevap:
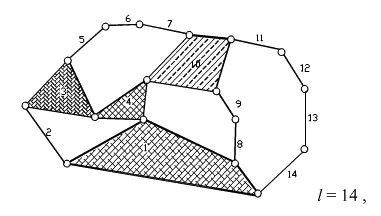
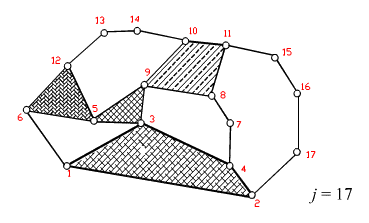
Olduğuna gore L=17-14+1=4
Dört adet bağımsız devre vardır.
Örnek:
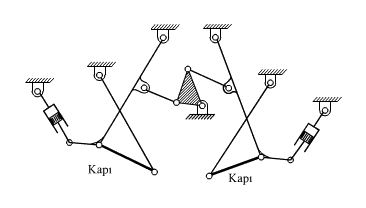
Kapı açma mekanizmasında kaç bağımsız devre vardır?
Cevap:
l=15 ve j=19 olduğuna göre, L=20-14+1=5 dir.