Kompleks Sayılar

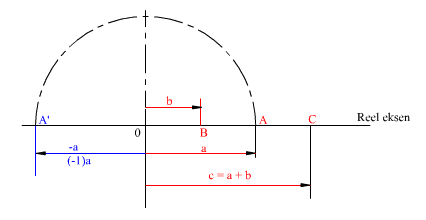
Reel sayılar hayatta ağırlık, uzunluk gibi değerlerin miktarını veya boyutunu göstermek için kullanılır. Adet belirten durumlarda reel sayıların tam sayı olması gerekir. Ölçüm aletlerinde, gösterdikleri miktara göre bu sayı bir kadranda gösterilir.Kadran, bir doğru veya bir daire yayı üzerinde belirli bir uzunluğun ölçülen değerinin belirli bir değerine karşı gelecek şekilde ölçeği önceden belirlenmiş bir benzeştirme şeklidir. Öyle ise, bir reel sayı 0 noktası başlangıç noktası olan bir doğru üzerinde noktalar olarak gösterilebilir. a ve b gibi iki sayıyı toplamamız gerekiyor ise, 0 noktasından a noktası uzunluğunu işaretler ve bu noktadan başlayarak b uzunluğunu yerleştiririz. Bu bize c=a+b değerini verecektir

Genelde 0 noktasından sağa doğru ölçülen değer pozitif reel sayı içindir. Bu durumda negatif reel sayılar aynı doğru üzerinde 0 noktasından sola doğru ölçülecek ve pozitif sayıdan (-1) oparatörü ile elde edilecektir. OA ve OA' uzunluklarının şiddeti eşit olup birbirlerine göre 180^o açı yapmaktadırlar. Yani a gibi bir pozitif sayıyı ele alır, bu sayıyı gösteren OA doğrusunu O etrafında 180^o döndürür isek, OA' noktasına yani -a ya varırız. (-1) oparatörüne bu açıdan bakdığımızda bir reel sayıya (-1) oparatörü etki ettiğinde, sayının geometrik gösterimi olan OA doğrusu O etrafında 180^o dönecektir. Eğer (-1) oparatörü bir sayıya arka arkaya iki defa etki eder ise, OA değişmez çünkü 180^o döndürme iki defa üst üste yapıldığından OA 360^o dönmüş ve aynı noktaya gelmiştir ((-1) x (- 1)=1).

Şimdi yeni bir oparatör yaratalım ve buna (i) diyelim. Bu operatör bir sayıya etki ettiğinde sayıyı gösteren doğru parçasını (-1) gibi 180^o değil, 90^o saat yelkovanına göre ters yönde döndürsün. Eğer bu oparatör bir sayıya iki defa etki eder ise sayıyı gösteren doğru 180^o (SYT) dönecektir. (-1) operatörü tanımımıza ters düşmemek için i.i = i² = -1 olmalıdır. Bu durumda i =olması gerekir. i ile işlem görmüş bir sayı sanal sayı olarak adlandırılır.

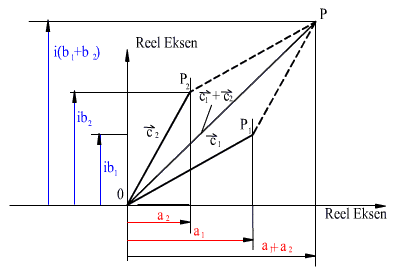
a ve b gibi iki reel sayı düşünelim.. Eğer b üzerine 90^o (SYT) dönme işlemi için i operatörü etki eder ise, ib elde edilir ve yukarıda gösterildiği gibi, ib, OB' doğrusudur ve OB uzunluğunda olup OB ye göre 90^o saat yelkovanına ters yönde döndürülmüştür. Şimdi c= a + i b toplamını göz önüne alalım. Bu gösterim bize a yı gösteren uzunluk ile b yi gösteren uzunlukları göz önüne almamızı, a uzunluğuna b uzunluğunu 90^o (SYT) döndürdükten sonra eklememizi söylemektedir. Geometrik olarak bu değer bize düzlemde bir P noktasının konumunu, 0 noktasına ve tanım-ladığımız reel eksen doğrusuna göre belirleyecektir. c kompleks sayı olarak tanımlanır. c sıralı bir çift (a, b) sayıdır ve geometrik olarak düzlemde her hangi bir nok-tayı gösterebilir. Kompleks sayının reel kısmı a, sanal kısmı ise b dir. Oluşan düzleme Gauss-Argand, Cauchy düzlemi veya kompleks sayı düzlemi denir. Öyle ise bir kompleks sayı etkili bir şekilde düzlemde bir noktanın konumunu bir konum vektörü gibi gösterebilir. Kompleks sayı vektör değildir (vektör operasyonları tanımlı değildir), ancak düzlemde konum vektörü olarak kullanılması çok büyük kolaylıklar getirmektedir.

Bir kompleks sayının mutlak değeri, r, O merkezinden kompleks sayının tanımlamış olduğu P noktasına uzaklıktır (OP) ve r =OP= dir. kompleks düzlemde bu sayının modülüdür. OP ile reel eksen arasında kalan ve daima saat yelkovanı yönüne ters ölçülen açı ise (), kompleks sayının argümanıdır.

Kompleks sayılarla ilgili şu önemli hususları belirtebiliriz:

a)	İki kompleks sayının reel ve sanal kısımları ayrı ayrı eşit ise veya modül ve argümanları aynı ise birbirlerine eşittir.
b)	Kompleks sayılar vektörel toplama kuralına uyarlar. İki kompleks sayının toplamı reel ve sanal kısımlarının ayrı ayrı toplamı ile elde edilir. Eğer c1= a1+ib1 ve c2= a2+ib2 iki kompleks sayı ise, toplam z: z=c1+c2= (a1+a2)+i(b1+b2) dir.
c)	Kompleks sayıların çarpımı ve bölümü temel cebir kurallarına göre yapılır. Burada tek fark i2=-1 olmasıdır. Kompleks sayıyı: c=a+ib

şeklinde göstermek ortogonal gösterimdir. Şekilden:

a=rcos, b=rsin

olduğu görüldüğünden:

c=r(cos+isin)

veya Euler denklemi: = cos +i sin kullanıldığında, c kompleks sayısı:

c =r

olarak yazılabilir. Bu yazılım kompleks sayının üstel gösterimi veya polar gösterimidir.

Eğer bir kompleks sayının modülü 1 birim ise ( r =1 ):

u =

dir. Bu birim vektör pozitif reel eksen ile SYT yönünde kadar bir açı yapmaktadır.

c = OP = r kompleks sayısını bir reel sayı (k) ile çarptığımızda:

c' =OP'= kc = k

bu çarpım sonucu elde ettiğimiz c' kompleks sayısında arguman c kompleks sayısı ile aynı olup modul kr olmuştur. Öyle ise OP uzunluğu bu reel sayı ile yapılan çarpımda "uzamış" (veya kısalmış) tır (alttaki şekil). Bir reel sayı ile çarpım uzatma oparasyonu olarak tanımlanacaktır. Bu oparasyon ile bir kompleks sayının şiddeti (modülü, boyutu) yönü aynı kalmak şartı ile artırılıp eksiltilebilir.

Eğer c =r kompleks sayısını birim vektörü gösteren bir kompleks sayı, u = ile çarpar isek:

c" = OP" = u.c = . r

dir. Temel cebir kurallarını uyguladığımızda (aynı tabanlı iki sayı çarpıldığında üstler toplanır):

c" = r

olacaktır. Şimdi ise, c vektörünün şiddeti aynı kalmış açısı ise iken bu çarpım ile + olmuştur. Başka bir deyiş ile OP vektörü O merkezinden SYT yönünde açısı kadar dönmüştür (üstteki şekil). Bu durumda, ile çarpım bir döndürme oparasyonudur ve bir döndürme oparatörüdür. (Dikkat edilir ise = i   ve dir ve bu birim vektörler kompleks sayı ile çarpıldığında vektörü sırası ile 90^o ve 180^o SYT yönünde döndürür. Yani dönme oparatörü önceden tanımlamış olduğumuz i ve -1 oparatörlerinide içermektedir).

Bir kompleks sayının kompleks eşleniğinde reel ve sanal kısımlarının şiddeti kompleks sayı ile aynıdır, ancak kompleks eşleniğin sanal kısmı kompleks sayı ile ters işaretlidir. Yani c=a+ib ise,bu kompleks sayının kompleks eşleniği =a-ib dir veya polar gösterimde c=r ise, kompleks eşlenik =olur (alttaki şekil).

Bir kompleks sayının kompleks eşleniği reel eksene göre kompleks sayının ayna görüntüsüdür.

Kompleks eşlenik kullanılarak:

r² = c= (a+ib) (a-ib) = a² +b²

Kompleks sayının reel kısmı:

Kompleks sayının sanal kısmı:

Eğer c₁= a₁+ib₁ ve c₂= a₂+ib₂ ise, kompleks sayılarının birbirleri ile bölümü:

bu terimi sadeleştirmek için pay ve paydayı, payın kompleks eşleniği ile çarptığımızda:

olur.