2.1 Mekanizma Serbestlik Derecesi-3
Bir Mekanizmanın serbestlik derecesini belirlerken
belirlememiz gerekecektir.
Uzuv Sayısını belirlerken bir uzvun birden fazla parça kullanılarak imal edilebileceğini hatırlayalım. Eğer bir veya birkaç cisim arasında bağıl hareket yok ise, bu cisim kümesi tek bir uzuvdur.
Mafsal sayısı ve tipini belirlerken temas sayısı ve şekli önemli değildir. Önemli olan husus mafsal ile birleştirilen kinematik çiftler arasında bulunan bağıl harekettir.

Mafsallar imal edilirken yük taşıma kapasitesine ve uygulamaya göre farklı olabilir. Yukarıda gösterildiği gibi, pim farklı uzuv ile sabitlenmiş ve farklı uzuv ile döner çift oluşturmak için yataklanmış olabilir. Temas yüzeyi sayısı farklıda olabilir.
|
|
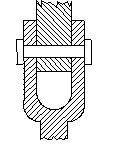 |
Yük taşıma özelliklerini artırmak için iki uzuv arasında birden fazla
temas sağlanabilir. ![]() Her temas ayrı bir
kinematik çift demek
değildir. İki uzuv arasında sadece bir kinematik çift olabilir.
Her temas ayrı bir
kinematik çift demek
değildir. İki uzuv arasında sadece bir kinematik çift olabilir.
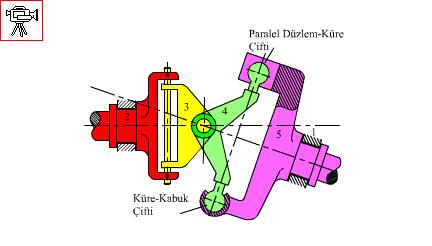
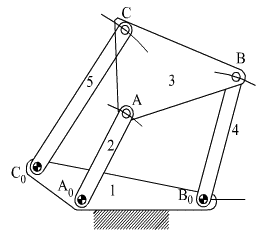
Yukarıda gösterilmiş olan uzaysal mekanizmada 4 ile 5 uzvu arasında birisi küre-kabuk, diğeri ise paralel düzlem-küre olmak üzere iki kinematik çift görülmektedir. Ancak iki uzuv arasında bağıl hareket belirlenirken 4 ve 5 uzvu arasında tek mafsal düşünülmesi gereklidir. Küre-kabuk çiftinden dolayı iki uzuv arasında üç eksende dönme serbestisi vardır (eksenler küre merkezinde çakışır). Paralel düzlem-küre çiftinden dolayı ise iki uzuv arasında beş serbestlik vardır. İki uzuv arasında bağıl serbestlik, serbestlik derecesi en düşük mafsaldan fazla olamaz (eğer kısıtlanan hareketler her temas noktasında aynı ise serbestlik derecesi en düşük serbestlik derecesidir) . Bu durumda serbestlik derecesinin üçten fazla olması beklenmemelidir. Ancak Paralel düzlem-küre çiftinin konumuna baktığımızda, bu mafsal resim düzlemine dik bir eksende ötelemeye müsaade etmeyecektir. Bu öteleme mümkün olamayınca küre kabuk çiftinin bir dönme serbestiside kısıtlanacaktır. Bu durumda iki uzuv arasında bu iki temastan dolayı kamalı küre kabuk çifti bulunmaktadır ve serbestlik derecesi ikidir (Küre kabuk merkezinden geçen şekil düzlemine dik bir eksende ve iki küre küre merkezini birleştiren doğru etrafında dönme).
Mekanizma uzuvları uygulamaya bağlı olarak çok değişik şekillerde üretilebilirler.
|
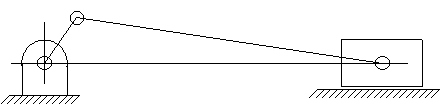
Bu, krank-biyel mekanizmasının şematik olarak gösterimidir
|
|
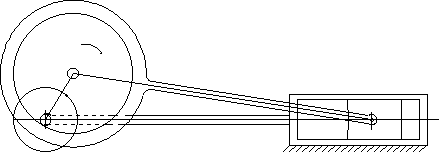
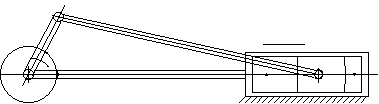
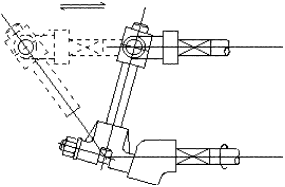
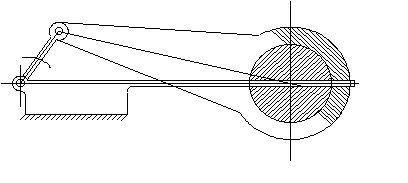
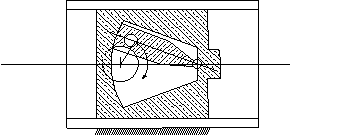
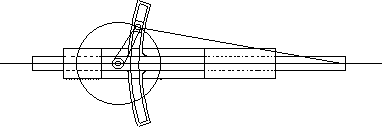
Aşağıdaki şekiller ise, farklı uygulamalarda parçaların farklı tasarımı ile elde edilebilecek mekanizmanın teknik resmidir.
|
 |
 |
 |
|
Uygulamada kullanılan malzemeye, uygulama alanına göre mekanizma uzuvları daha farklı şekiller alabilir. |
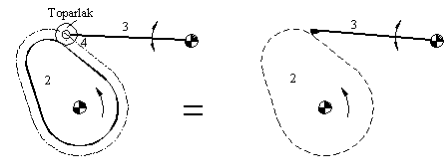
Kam mekanizmalarında genellikle izleyici uzuv ucunda bir döner mafsal ile toparlak olarak adlandırılan bir uzuv bulunur ve uzuv karşı uzva bir kam çifti ile bağlıdır. Eğer bu mekanizmanın serbestlik derecesi hesaplanır ise 4 uzuvlu, 3 döner mafsal ve bir kam çifti (j=4, Sfi=5) olan bu mekanizmanın serbestlik derecesi (F=3(4-4+1)+5=2) 2 olacaktır. Bu değer, ilk bakışta yanlış görülse bile doğrudur. Çünkü bir parametre pratikte kam olarak adlandırılan 2 uzvunun dönme hareketi ile belirlenir iken, 4 uzvunun kam üzerinde hem kayma hemde yuvarlanma yapabilmesinden dolayı ek bir serbestisi bulunmaktadır. Pratikte bu toparlağın kullanılması ile kam yüzeyinde sadece yuvarlanma olacak ve sürtünme kayıpları en aza indirgenecektir ancak kinematik açıdan toparlak uzvuna gerek yoktur ve giriş - çıkış uzuvları arasında hareketin incelenmesi sırasında toparlak uzvu ihmal edilerek eşdeğer harekete sahip 3 uzuvlu mekanizmanın serbestlik derecesi bulunur.
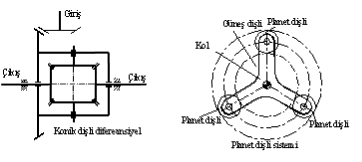
Diğer bazı mekanizmalarda daha uygun kuvvet iletimi için parça sayısı artırılabilir. Buna en uygun örnek planet dişli sistemleridir. Kinematik açıdan tek bir planet dişli kullanılması yeterli olduğu halde, yük dağılımını daha iyi bir duruma getirmek, atalet kuvvetlerini dengelemek ve daha fazla moment iletimi için genellikle iki veya daha fazla planet dişli kullanılır. Bu şekilde planet dişlilerin çalışabilmeleri için planet dişlilerin çapı ve diş sayısı aynı olmalıdır. Aksi takdirde planet dişli kilitlenecektir. Kinematik açıdan aynı kola bağlı planet dişli gurubundan birisi düşünülmeli diğer planet dişli gurubu göz önüne alınmamalıdır. Sistem bu şekilde ele alındığında serbestlik derecesine kinematik açıdan uyacaktır.
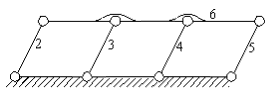
Genel olarak bir mekanizmanın serbestlik derecesi, o mekanizmada bulunan uzuvların boyutlarına bağlı değildir. Ancak bazı durumlarda mekanizmanın serbestlik derecesi uzuv boyutlarına bağlı olabilir. Örneğin, Şekil 1.30 da gösterilen düzlemsel mekanizmada 6 uzuv, 8 döner mafsal olduğuna göre serbestlik derecesi: F=3(6-8-1)+8=-1 ise de, mekanizmada oluşan dörtgenlerin karşı kenarları birbirlerine eşit ise (ki bu nedenle bu tip mekanizmalar parallelogram mekanizması olarak adlandırılır), mekanizma hareket edebilir. Serbestlik derecesi denkleminden elde edilmiş olan serbestlik derecesi, eğer uzuv boyutları farklı değerlerde olsa idi, geçerli olacaktı. Bu tür mekanizmalara kritik boyutlu mekanizmalar diyeceğiz. Kritik boyutlu mekanizmalarda genellikle paralel kenarlı dörtgen halkalar görülecektir. Düzlemsel kritik boyutlu mekanizmalar parallelogram mekanizmalarından farklı olarak 4. kısımda görülecek olan Robert-Çebişev teoremi ile de elde edilir.

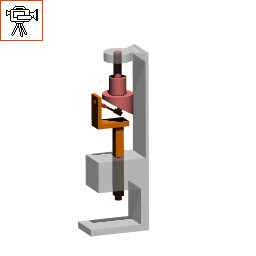
Yukarıda serbestlik derecesi denklemine göre eksi serbestlik derecesi olan çok kafalı matkap örneği görülmektedir. Paralelogram mekanizması kullanılarak dönen bir giriş milinden aynı hızda dönen dört çıkış mili elde edilmektedir (geretiğinde çıkış mili sayısı daha fazla olacak şekilde tasarlanabilir). Bu ancak uzuvların birbirlerine eşit ve paralel olmaları durumunda mümkündür.
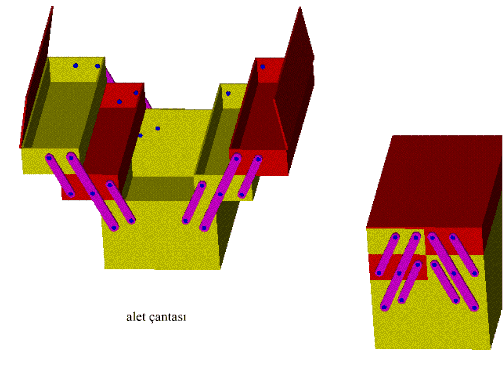
Anlık kritik boyutlu mekanizma ise, mekanizma sadece tasarım konumunda sınırlı bir miktar hareket edebilir, diğer konumlarda ise mekanizma bir rijit yapı oluşturmaktadır. Bu tip mekanizmaların serbestlik derecesi sıfır veya eksi değerde-dir. Ancak özel uzuv boyutlarından dolayı, tasarım konumlarında belirli bir miktar hareket serbestileri bulunur. Bu hareket serbestisi, uygulamada mafsal boşlukları ve uzuv esnekliklerinin eklenmesi ile önemli bir miktar olur. Bu mekanizmalar ağır yüklerin sınırlı mesafelerde taşınması gibi durumlarda kullanılır.
Kritik boyutlu uzay mekanizmaları kullanımda oldukça yaygındır. Bu mekanizmaların, serbestlik derecesi denklemine göre hareket etmemesi gerekirken hareket etmesi, çoğunlukla uzayda eksenlerin bir veya bir kaçının çakışması veya parallel olması ile sağlanır. Kritik boyutlu uzay mekanizmaları için bazı örnekler aşağıda verilmiştir. Eğer mekanizmada bulunan mafsalların eksenleri tek bir noktada çakışır ise, bu tür mekanizmalar uzaysal değil küresel mekanizmalar olarak adlandırılmaları gerekir ve küresel mekanizmaların uzay serbestlik derecesi 3 olarak alınmalıdır. Bu durumda mekanizma uzuvları üzerinde bulunan noktalar aynı merkezli küre yüzeyleri üzerinde hareket ederler.
Uzaysal mekanizmalarda daha başka kritik durumlar mevcuttur. Ancak serbestlik derecelerinin bulunması, mekanizmanın kinematik analizinin yapılması ile mümkün olur.
|
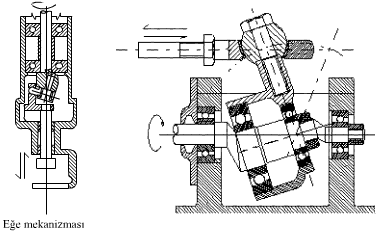
teknik resim |
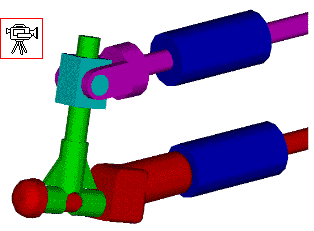
katı model |
Yukarıdaki mekanizmada mekanizmanın çalışabilmesi için döner mafsal eksenleri ve slindir çift ekseni bir noktada kesişmesi gerekir.
Eğer bir düzlemsel kinematik zincir sadece kayar ve döner kinematik çiftlerden oluşuyor ise, Mekanizma uzuvlarının hareketi belirli olabilmesi için kinematik zincirde aşağıda verilmiş olan kuralların sağlanması gerekir:
- Eğer bir uzvun kinematik elemanları sadece kayar mafsal oluşturuyor ise, kayar mafsalların tümü parallel olamaz. Çünkü bu durumda mekanizmanın diğer kısımlarının serbestlik derecesi ne olursa olsun, bu uzuv kayar mafsal eksenleri doğrultusunda mutlaka hareket edebilecektir.
- İki kinematik elemanlı ve sadece kayar mafsal oluşturan iki uzuv doğrudan birbirleri ile bağlı olmamalıdır. Bu durumdada bu iki uzuv, diğer mekanizma uzuv ve mafsallarına bağlı olmadan mutlaka hareket edebilecektir (ileride görüleceği gibi, mekanizmanın bu kısmında uzay serbestlik derecesi iki olur).
- Kinematik zincir içinde bulunan hiç bir halkada döner mafsal sayısı ikiden az olamaz. Döner mafsalın bir olduğu bir durumu ele alırsak diğer mafsallar kayar mafsal olduğundan o uzuvlar arasında bir dönme hareketine müsaade edilemeyecektir. Bu durumda tek döner mafsal olması durumunda bu mafsalda bağıl dönme hareketi olamı-yacağından böyle bir halkanın zincir içinde bulunmaması gerekir.
- Sadece döner ve kayar mafsallardan oluşan bir mekanizmada üç uzuvlu bir halka bir rijit cisimdir. Çünkü bu durumda bu uzuvlar arasında bağıl hareket mümkün değildir.
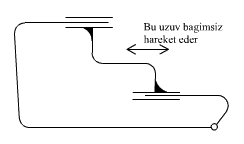
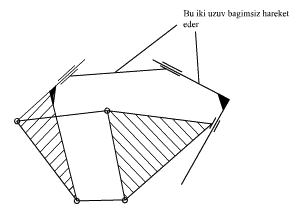
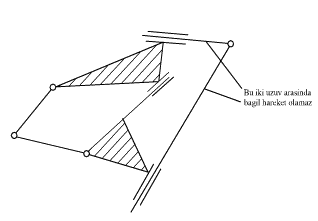
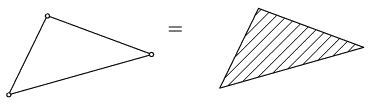
Yukarıda gösterilen özel durumlarda, mekanizmanın bir kısmında ya kontrol edilemiyen serbestlik (1 ve 2) ya da hareketsizlik (3 ve 4) bulunmaktadır.
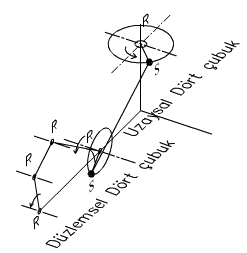
Mekanizma serbestlik derecesi denkleminin kullanılamıyacağı, veya kulla-nıldığında yanlış sonuç vereceği bir durum ise uzay serbestlik derecesinin tüm mekanizma için aynı olmadığı durumlardır. Örneğin bir uzaysal dört-çubuk mekanizmasına bu mekanizmanın çıkış uzvu ile tahrik edilen bir düzlemsel dört çubuk mekanizması ekliyelim. Sonuçta elde edilen mekanizma bir serbestlik dereceli olacaktır. Ancak serbestlik derecesi denklemini uygulamak istediğimizde uzay serbestlik derecesinde bir belirsizlik olacaktır. Çünkü mekanizmanın belirli bir kısmı düzlemsel iken belirli bir kısmı uzaysaldır. Bu nedenle genel serbestlik derecesi hatalı sonuç verecektir.
 |
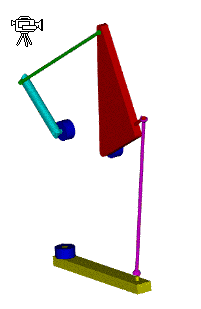 |
|
teknik resim
|
katı model
|