- Alt Bağlama Açısı Problemi

"Verilen bir salınım açısını () ve buna karşı gelen bir krank dönme açısını () sağlayan, ve ayrıca bağlama açısının 90⁰ den sapması en az olan kol-sarkaç oranlarında dört- çubuk mekanizmasının boyutlarını belirleyin."

Problem iki kısımdan oluşmaktadır:

1.	Verilen bir salınım açısını () ve buna karşı gelen bir krank dönme açısını () sağlayan kol-sarkaç mekanizmalarının bulunması,
2.	Elde edilen kol-sarkaç mekanizmaları arasında bağlama açısı en iyi olan kol-sarkaç mekanizmasının belirlenmesi.

1-Verilen bir salınım açısını () ve buna karşı gelen bir krank dönme açısını () sağlayan kol-sarkaç mekanizmalarının bulunması:

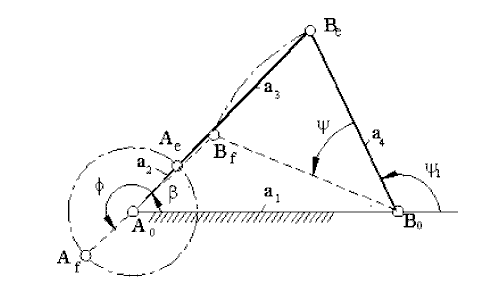
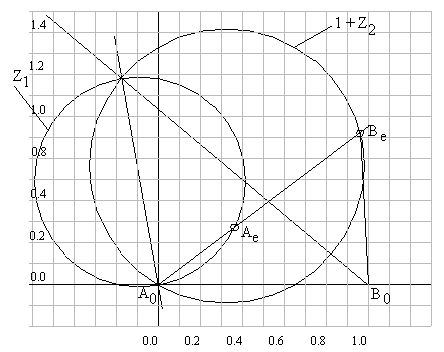
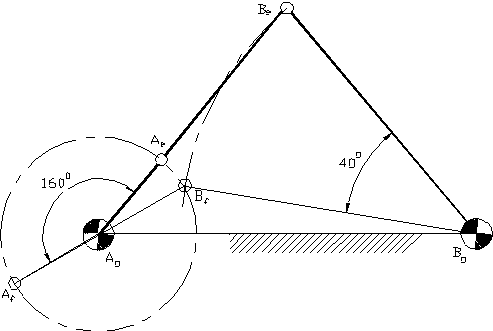
Kol-sarkaç mekanizmasını iki ölü konumda çizelim. Her iki konumda krank ve biyel uzuvları aynı doğrultudadır. Açık konumda biyel açısı krank açısına eşittir, kapalı konumda ise krank açısından 180⁰ farklıdır. Bu konumlar için devre kapalılık denklemlerini yazalım.

	(7)
	(8)

bu denklemler:

	(9)
	(10)

şeklinde yazabiliriz. Z₁, Z₂ ve yeni parametreler olup:

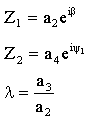
olarak tanımlayalım Z₁ ve Z₂ A₀A_e ve B₀B_e vektörlerini gösteren kompleks sayılardır ise biyel uzuv boyutunun krank uzuv boyutuna oranıdır. Önceden söylenildiği gibi uzuv boyutları belirli bir ölçekle büyültülüp küçültüldüğü halde dönme açıları değişmiyeceğinden, sabit uzuv boyutunu bir birim alalım (a₁=1 ). Şimdi ölü konumlar için devre kapalılık denklemleri:

(1+)Z1 - Z2 = 1	(11)
	(12)

olacaktır. Kinematik analiz problemlerinin aksine, şimdi bu denklemlerde ve açıları bilinen değerler olup bu değerler için mekanizma boyutlarını bulmamız gerekmektedir. Bu iki kompleks sayılarla yazılmış olan denklem Z₁ ve Z₂ parametreleri için lineer bir denklem takımını oluşturur. Çözümü bilinen Kramer kuralı ile yapıldığında:

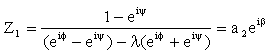	(13)
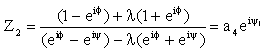	(14)

elde edilir. değeri - dan +a kadar değişik değerler aldığında, Z₁ ve Z₂ vektörlerinin uç noktaları bir eğri çizecektir. Ve bu uç noktalar A_e ve B_e noktalarının geometrik yerleridir. Bu geometrik yerler verilen ve değerlerine göre bir dairedir. Örneğin =160⁰ ve =80⁰ için bu iki daire aşağıda gösterildiği gibi çizilmiştir (bu iki daireyi aynı sabit eksen referansında çizmek için A₀ merkezli ve x ekseni sabit uzuv ile çakışan bir referans eksen alınmıştır. Bu durumda Z₂ vektörü yerine 1+Z₂ vektörü bu eksen takımında bize B_e nin geometrik yerini vereceğinden bu vektör çizilmiştir). Görüldüğü gibi her bir oranı farklı bir çözüm verecektir ve sonsuz sayıda çözüm vardır. Ancak kol sarkaç oranı için krankın en küçük uzuv olması gerektiğinden >1 gerekli bir şarttır ve dairelerin belirli bir kısmı için bu geçerlidir. Elde edilen konum ölü konum olduğundan, A₀, A_e ve B_e bir doğru üzerinde olması gerekir. Öyle ise, parametresi yerine A₀ dan A₀B₀ doğrusuna açısı yapan bir doğru çizelim. Bu doğru daireleri A_e ve B_e noktalarında kesecektir ve mekanizma ölü konumda elde edilecektir. Bu durumda bağımsız parametre olacaktır ve geometrik olarak uzuv boyutları şekilden: A₀A_e=a₂, A_eB_e=a₃, B₀B_e=a₄, A₀B₀=a₁=1 bulunacaktır. açısı krankın ölü konum açısıdır.

Yukarıdaki eğriyi geometrik olarak çizme yöntemini öğrenmek için alttaki animasyonu inceleyiniz.

Uzuv boyutlarını parametresine göre analitik olarak elde etmek istediğimizde:

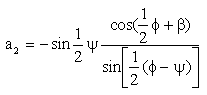	(15)
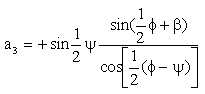	(16)
	(17)
a1 = 1

denklemleri kullanılabilir. parametresine göre ise uzuv boyutları denklem 13 ve 14 kullanılarak:

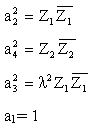
elde edilir. Verilen bir salınım açısı ve karşı gelen bir krank dönme açısına göre veya parametresi kullanılarak istenilen açıları sağlayan sonsuz sayıda mekanizma elde edilebilmektedir. Kol-sarkaç oranlarının sağlanabilmesi için ayrıca sarkaç salınım açısı:

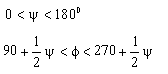
denklemlerini sağlamalıdır. ve parametrelerinden elde edilebilecek t,u ve v parametrelerini:

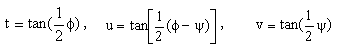
tanımlayalım. Bu yeni parametreler kullanılarak uzuv boyutlarını şu şekilde gösterebiliriz:

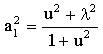	(18)
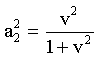	(19)
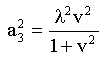	(20)
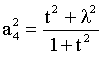	(21)

Örnek

Sabit uzuv boyu 120 mm olan, salınım açısı =40⁰ ve buna karşı gelen krank dönme açısı =160⁰ olan bir kol-sarkaç mekanizmasını ve bulunan mekanizmanın kritik bağlama açısını bulun.

a) Krank ölü konum açısını = 60⁰.olarak seçelim. (15)-(17)denklemlerini kullanarak:

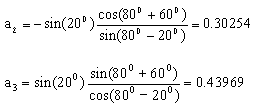
ve

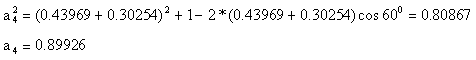
a₁=120 mm olduğunda , a₂=36.30 mm, a₃=52.76 mm ve a₄=107.91 mm olacaktır.

Bağlama açısının 90⁰ den en fazla sapması ise denklem (4) kullanılarak:

Buradan : _max=151.44⁰ (₁=61.44⁰) ve _min=49.32⁰ (₂=40.68⁰) elde edilecektir. _max ın 90⁰ den sapması 61.44⁰ olduğundan mmax göz önüne alınması gereken kritik bağlama açısıdır.

b) Eğer biyel uzunluğunun krank uzunluğuna oranı = 1.4 olarak seçilir ise, (18)-(21) denklemlerini kullanarak:

       t = tan(80⁰)=5.671282, u = tan(60⁰)=1.732051, v = tan(20⁰)=0.36397

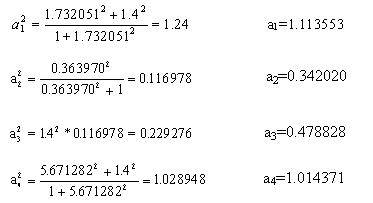
elde edilir. a₁=120 mm olduğunda: a₂=(0.342020/1.113553)*120=36.86 mm, a₃=51.60 mm, a₄=109.31 mm olacaktır. Bu mekanizma için kritik bağlama açısı denklem (4) den:

Buradan : _max=152.36⁰ (=62.36⁰) ve _min=49.96⁰ (=43.04⁰). _max ın dik açıdan sapması 62.36⁰ olduğundan _max kritik bağlama açısıdır.

Görüldüğü gibi, istenilen sarkaç salınım açısı ve karşı gelen kol dönme açısını sağlayan sonsuz sayıda kol-sarkaç mekanizması elde edilebilecektir. Elde edilen her mekanizmanın bağlama açısı farklı olacağından 90⁰ den sapmalarıda farklı olacaktır. Basit bir çalışma olarak l veya b parametrelerinden birisi kullanılarak bu parametre serbest olduğundan değişik değerler verelim. Her bir değer için bağlama açısının 90⁰ den maksimum sapması farklı olacaktır. Bu sapmaların değişimini kullandığımız parametreye göre çizelim. Şekilde görüldüğü gibi bir eğri elde edilecektir. Dik açıdan sapmanın en az olduğu mekanizma bağlama açısı bakımından en iyi mekanizmadır ve onu seçtiğimizde uygulamada en az sorun ile karşılaşılacağı büyük bir ihtimaldir.

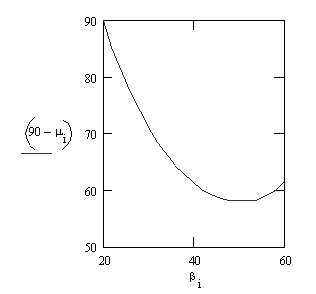
Bu en iyi bağlama açısına sahip mekanizmayı bulmak için her durumda yukarıda açıklanan yöntemi izlemektense, uzuv boyutları tek bir parametre ile () ifade edilebildiğine göre bağlama açısı da sadece bu parametrenin fonksiyonu olacaktır. (4) numaralı denklemde:

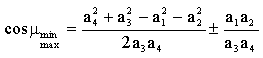(4)

uzuv boyutlarını ile ifade eden (18)-(21) numaralı denklemler kullanılır ise, bağlama açısı bu parametre ile ifade edilmiş olacaktır. Bağlama açısının dik açıdan sapmasını minimum veya maksimum edecek değerine (_opt) dersek, denklem (4) ün ya göre türevini alıp sıfıra eşitlediğimizde elde ettiğimiz değer bu en iyi durumu içerecektir. Bu işlem yapıldığında _opt değeri:

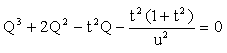(22)

Üçüncü derece denklemin köklerinden birisi olarak elde edilir. Bu denklemde 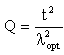dur ve denklemin üç kökünden olanı kol-sarkaç oranını sağlayacağı gibi, bu (_opt) değeri kullanılarak elde edilen kol-sarkaç mekanizmasının bağlama açısı diğer değerleri kullanılarak elde edilecek kol-sarkaç mekanizmalarına göre dik açıdan en az sapma gösterecektir.

(22) numaralı denklem basit Newton-Raphson iteratif yöntemi ile çözülebilir. Kök aralığı orta noktası ilk tahmin alınarak (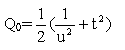) ve bu kökün bulunması için tekrarlama denklemi:

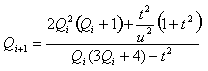(23)

kullanılarak yeni köke daha yakın değerler elde edilebilir. İterasyona 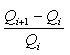yeteri kadar küçük olduğunda (örneğin 10^-6dan küçük) son verilir.

Bir salınım açısı ve karşı gelen kol açısına göre en iyi bağlama açısı değerlerini veren kol ölü konum açısı ve en iyi bağlama açısı değerler grafik olarak Abak 1 de görülmektedir (bu abak ilk olarak Alt tarafından hazırlanmış, soradan Volmer tarafından düzenlenmiştir. Bu nedenle Alt diyagramı denmektedir). Bu abak kullanılarak kol ölü konum açısı ve en kritik bağlama açısının en iyi değeri maxmmin verilmektedir. Uzuv boyutları bu abaktan elde edilen değerinin (15)-(17) numaralı denklemde kullanılması ile elde edilir.

Örnek

Sabit uzuv boyutu 120 mm, salınım açısı =40⁰ ve karşı gelen krank dönme açısı =160⁰ olan ayrıca en iyi bağlama açısına sahip kol-sarkaç mekanizmasını bulun.

Verilen açılar kullanılarak t=5.671282 ve u=1.732051 bulunur, öyle ise aranan kök: 0.333333<Q<32.163437 aralığındadır. Q₀=16.248 alalım ve titerasyon denklemi kullanarak:

Öyle ise aranan kök (6 basamak doğrulukta): Q=7.855706 dir. Buna göre _opt=2.023432 bulunur. Bu _opt değeri uzuv boyutlarını bulmak için kullanıldığında:

a₁=120 mm olduğunda : a₂=(0.342020/1.331754)*120=30.82 mm a₃=62.36 mm, a₄=94.22 mm olarak bulunur. Bu mekanizma için bağlama açısının dik açıdan en fazla sapması ise:

Bu denklemden : _max=114.170 (₁=24.170) ve _min=31.850 (=58.150). _min daha fazla sapma gösterdiğinden _min kritik bağlama açısıdır. Verilen salınım açısı ve karşı gelen kol dönme açısını sağlayan ve bağlama açısı dik açıdan en az sapan mekanizma boyutları bu elde edilmiş olan boyutlardır. Farklı bir veya parametre değeri ile bulunan kol-sarkaç mekanizmasının bağlama açısının dik açıdan sapması bu bulunan mekanizmadaki sapmadan mutlaka daha fazla olacaktır.

Abak 1'e baktığımızda ise, verilen =40⁰ ve =160⁰ değerleri için abakdan: max(_min)32⁰ ve 50.5⁰ okunabilir. Tabii ki abaktan sınırlı bir hassasiyetle okumak mümkündür. Uzuv boyutlarını bu b değeri ile bulduğumuzda: a₁=1, a₂=0.2565, a₃=0.5201 and a₄=0.784 değerlerini elde ederiz. a₁=120 mm olduğunda; a₂=30.78 mm, a₃=62.41 mm and a₄=94.08 mm bulunur. Sonuç mekanizma şekilde gösterilmiştir.

Yukarıda anlatılmaya çalışılmış olan ölü konumlara göre(verilen herhangi bir ve değerine göre) bir kol-sarkaç mekanizması tasarımı için hazırlanmış olan Excel kütüğünü alabilirsiniz.

Yukarıda verilmiş olan genel çözümün dışında iki özel durum oluşmaktadır. Bunlardan birisi santrik kol-sarkaç mekanizmasıdır.bu durumda ölü konumlar arasında kol dönme açısı =180⁰ dir ve bağlama açısının maksimum ve minimum değerleri:

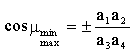
dir. Eğer dik açıdan sapmanın en az olması istenir ise a₂=0 olması ( a₁=1 alınmıştı) veya a₃ veya a₄ uzuv boyutlarından birisinin sonsuz olması gerekir. Pratikte bu durumlar mümkün olamıyacağından, bağlama açısı ve uzuv boyutları arasında oran makul değerlerde olacak şekilde kol-sarkaç mekanizması boyutlarını ararız. (örneğin bağlama açısının dik açıdan sapması değerinin büyümesi ile azalacaktır).

İkinci özel durum ise -=180⁰ olmasında rastlanılır (). Bağlama açısının optimum değeri: 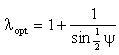olacaktır ve uzuv boyutları:

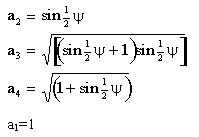
olur.